Elias Gamma encoding

Anatoliy Kuznetsov. 2009. UPDATE: Jan.2020

Introduction

BitMagic Library v.3.6.0 implements a variant of Elias Gamma Encoding as part of bit-vector serialization. Wikipedia has an article on this encoding: http://en.wikipedia.org/wiki/Elias_gamma_coding

Older versions of BM library used D-Gap compression which is a variant of run length encoding. Or used plain lists of integers to encode very sparse sets. All this compression methods used word aligned algorithms and rely on presence of long runs of identical bits.

D-Gap encoding

In certain cases, bit blocks will frequently have a non-random bit distribution pattern. Here's an example:

	0001000111001111

Patterns such as these can be represented in different ways. One of the most popular is a list of integers, each representing 1 bit. For example

	{ 3, 7, 8, 9, 12, 13, 14, 15, 16 }

This is a list of indexes of bits stored as an ascending sequence of integers.

Another common way of representing ascending sequences is by using the method of D-Gaps, the differences between elements of the list. Incidentally, this variant of D-Gap compression was used in the BitMagic library.

What is D-Gap Compression?

In D-Gap compression, the very first integer in the sequence is always 1 or 0, and it works as a flag indicating the start bit. In the example above the first bit is 0. The integers following the flag are the lengths of the consecutive blocks of equal bits. The sum of all elements of the sequence without the starting flag value will give us the total length of the block. Essentially this coding model can be treated as a specialized variant of Run Length Encoding (RLE). The D-Gap form of the previous example is:

	{[0], 3, 1, 3, 3, 2, 4}

This translates to "Three zeroes, one 'one', three zeros, three ones, two zeroes, and four ones", or

	000 1 000 111 00 1111

Older versions of BM library used D-Gap compression which is a variant of run length encoding or used plain lists of integers to encode very sparse sets. All this compression methods used word aligned algorithms and rely on presence of long runs of identical bits.

A lot of practical tests demonstrated that BM based search systems are bandwidth limited. It means that CPU is starved, waiting for memory operations or disk retrieval. Disk retrieval is particularly important because IO and network subsystems never followed terms of Moore Law. Non-Word-Aligned encoding seems to a good answer to this problem.

Elias Gamma Encoding

Elias Gamma encoding developed by Peter Elias postulates bit-encoding of positive (non-zero) integers. Positive non-zero integers are essentially the native format for BM library to store sparse bit-vectors or inverted lists (basic building blocks of efficient bitmap indexes).

Fragment of Gamma encoding table:

1 = 20 + 0 = 1                 
2 = 21 + 0 = 010                
3 = 21 + 1 = 011                
4 = 22 + 0 = 00100 
....

Here is our sequence of ints in the form on 16-bit native integers:
{3, 1, 3, 3, 2, 4}
{0000000000000011, 0000000000000001, 0000000000000011, 0000000000000011, 0000000000000010, 0000000000000100 }

Gamma code:
{011, 1, 011, 011, 010, 00100 }

Advantages

Simple implementation, requires no compression dictionary. It is easy to compress just a few ints without constructing and storing a dictionary. BM library works with independent blocks of bits (potentially computed in parallel).

Implied probability favors small integers â€“ good for BM library since it fragments bit-vector into blocks of 65K bits. Methods allows some blocks to be encoded, and some to remain in GAP or raw bit-block format (if statistical distribution of bits suddenly changes).

Compact implementation reduces code bloat, fits into a C++ template library paradigm.

Disadvantages

True adaptive statistical methods (like arithmetic compression) can(should?) give better compression ratio.

Encoding and decoding method is sequential, it seems hard to implement a parallel encoder/decoder using SIMD, SSE or GP-GPU. (BM blocks can potentially be decoded in parallel so maybe there is a way to use parallel methods for this).

Non-word-aligned scheme requires a lot of bit-shifting and masking, can be slow on some systems.

Usage example


        #include "bm.h"
        #include "bmserial.h"

        unsigned char* serialize_bvector(bm::serializer >& bvs,
                                         bm::bvector<>& bv)
        {
            // It is reccomended to optimize vector before serialization.
            bv.optimize();

            bm::bvector<>::statistics st;
            bv.calc_stat(&st);

            // Allocate serialization buffer.
            unsigned char*  buf = new unsigned char[st.max_serialize_mem];

            // Serialization to memory.
            unsigned len = bvs.serialize(bv, buf, 0);

            cout << "Serialized size:" << len << endl << endl;
            return buf;
        }

        int main(void)
        {
            bm::bvector<>   bv1;
            bm::bvector<>   bv2;

            .... Fill bit-vectors with values ....

            // Prepare a serializer class
            //  for best performance it is best to create serilizer once and reuse it
            //  (saves a lot of memory allocations)
            //
            bm::serializer > bvs;

            // next settings provide lowest serilized size
            bvs.byte_order_serialization(false);
            bvs.gap_length_serialization(false);
            bvs.set_compression_level(4); // Use Gamma encoding

            unsigned char* buf1 = serialize_bvector(bvs, bv1);
            unsigned char* buf2 = serialize_bvector(bvs, bv2);

            // Serialized bvectors (buf1 and buf2) now ready to be
            // saved to a database, file or send over a network.

            // ...

            // Deserialization.

            bm::bvector<>  bv3;

            // As a result of desrialization bv3 will contain all bits from
            // bv1 and bv3:
            //   bv3 = bv1 OR bv2

            bm::deserialize(bv3, buf1);
            bm::deserialize(bv3, buf2);

            delete [] buf1;
            delete [] buf2;

            return 0;
        }

UPDATE for v.5.0.0 and up

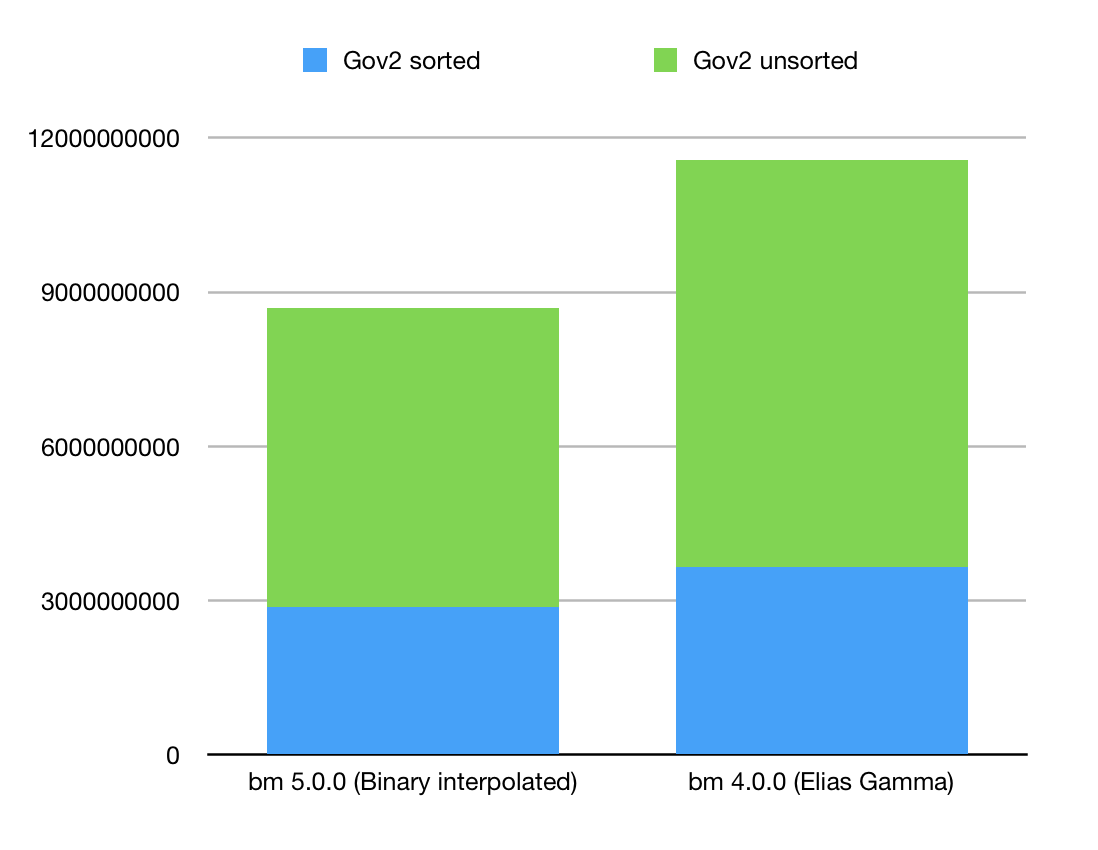
BitMagic v.5.0.0 implements a better compressed serialization of bit-vectors using Binary Interpolated Encoding (Center Minimal). Tested on Gov2 collection it gives approximately 25% improvement in disk footprint comparing to previous version which was using Delta Elias Gamma encoder. New serialization is backward compatible, BitMagic supports protocol evolution and will read old BLOBs. New serialization default is level 5. If you like to keep using Elias Gamma - use level 4.

Figure below illustrates new compression numbers using two Gov2 inverted list benchmark sets, sorted and unsorted.